PHY 133 homework, continued. (Reading refers to Serway & Jewett’s Physics for Scientists & Engineers
with Modern
Physics, 9th ed., “Hybrid Edition.”)
Sec. 5 - Special Relativity
Read:
A. 1. (2 points) The speed of an electron is
calculated from the voltage which accelerated it, using the formula KE = 1/2 mv2. In each case, state whether the answer is
correct to at least three significant figures:
a.
What if the answer is 5.00 x 108 m/s? ____________
b.
What if the answer is 1.00 x 108 m/s? ____________
c.
What if the answer is 5.00 x 107 m/s? ____________
d.
What if the answer is 1.00 x 107 m/s? ____________
2. (8) An observer on Earth sees spacecraft A
approaching Earth at .500c. An observer
on spacecraft A sees spacecraft B approaching him from behind at .600c. What does the observer on Earth see as the
speed of B?
ans:
.846c
B. 1. (2pts) A certain electron's total energy
is 1.17 MeV. What is its kinetic energy? ans:
.66 MeV
2. (8) A spaceship travels at .750c relative to
Earth. If the spaceship fires a small
rocket in the forward direction, how fast relative to the ship must it be fired
to travel at .950c relative to Earth?
ans:
.696c
C. 1. (2 pts) Explain in words why it is
impossible for an object (of nonzero mass) to reach a speed of c, regardless of
the size and duration of the force on it.
8. (8) Consider the decay 5524Cr
® 5525Mn + e, where e is an
electron. The 55Cr nucleus
has a mass of 54.9279 u, and the 55Mn nucleus has a mass of 54.9244
u. (a) Calculate the mass difference
between the two nuclei in electron volts.
(b) What is the maximum kinetic energy of the emitted electron?
ans:
3.26 MeV, 2.75 MeV
D. 1. (3 pts) An astronaut moves away from the
earth at a speed close to the speed of light.
What changes, if any, would be measured in the astronaut's size and
pulse rate by (a) an observer on Earth? (b) the astronaut?
2. Consider a
proton with an energy of 2.00 joules. (Cosmic ray particles have been seen with
this much or even a little more.) Assume
this proton has been moving with a constant velocity since leaving the center
of the Milky Way galaxy, 2.50 x 1017 km away as measured from the
Earth’s frame of reference. In the
proton’s reference frame,
a. What is the distance from the galactic center to the
Earth?
b. How fast is the Earth moving toward the proton? (A lengthy calculation is not necessary –
just think about what your value for γ means.)
c. How much time does the trip take?
ans:
1.88 x 107 km, c, 62.7 s
E. 1. (2 pts) What two speed measurements do two
observers in relative motion always agree on?
2. (8) The mass of a π– meson is 2.49 x 10 –28
kg and its average lifetime in its own frame of reference is 2.6 x 10 –8s. If the pion moves at .95c relative to an
observer on Earth, what will that observer measure for (a) its average
lifetime, (b) the average distance it travels before decaying? (c) its
momentum?
ans: 83.3 ns, 23.7 m, 2.27 x 10 – 19 kg·m/s
F. A pion at rest (mπ
= 2.4881 x 10 –28 kg) decays into a muon (mμ = 1.8835
x 10 –28 kg) and an antineutrino (![]() ≈ 0.) The reaction is written π–
→ μ– +
≈ 0.) The reaction is written π–
→ μ– + ![]() . It can be shown from
conservation of momentum that 12.15% of the energy produced by this decay goes
to the kinetic energy of the muon and the rest goes to the antineutrino. Find (a) the kinetic energy of the muon. (b) γ for the muon. ans:
6.60 x 10-13J, 1.04
. It can be shown from
conservation of momentum that 12.15% of the energy produced by this decay goes
to the kinetic energy of the muon and the rest goes to the antineutrino. Find (a) the kinetic energy of the muon. (b) γ for the muon. ans:
6.60 x 10-13J, 1.04
Sec. 6 - Wave-Particle Duality
Read: Ch 40: start – sec 2, sec 4, 5 & 8; Ch. 41: first part of sec 5, sec. 6
A. 1. (2 pts) Some stars look red, and some look
blue. Which has the higher surface
temperature? Explain.
2. (8) Molybdenum has a work function of 4.20
eV.
(a) Find the cutoff frequency and cutoff
wavelength for the photoelectric effect.
(b) Calculate the stopping potential if the light
has a wavelength of 180 nm.
ans:
1.02 PHz, 295 nm, 2.69 V
B. 1. (2 pts) A 3He nucleus and a 4He
nucleus, each with 4 MeV of kinetic energy, approach a thin barrier 5 MeV
high. Which, if either, is more likely
to tunnel through? (For ½mv2
to be the same, the lighter 3He is going faster.)
2. (8) Show that the de Broglie wavelength of an
electron accelerated from rest through a potential difference V is given by λ = ![]() . What is
the value of the constant if V is in volts and λ
is in nanometers? (Assume its speed is
non-relativistic.)
. What is
the value of the constant if V is in volts and λ
is in nanometers? (Assume its speed is
non-relativistic.)
ans:
1.226
C. The wave nature of particles was first
verified in 1927 when Davisson and Germer, at Bell Labs, demonstrated
diffraction of electrons from a crystal of nickel. Somewhat simplified data from one of their
trials is given below:
distance
between atomic planes: .81 ![]()
accelerating
voltage: 65 volts
a.
Find the electrons' speed from the accelerating voltage.
b.
Put the electrons' de Broglie wavelength into the Bragg equation to predict the
angle where the first order maximum would occur if de Broglie were correct.
ans:
4.78x106 m/s, 70° (Observed value = 68° - not a bad match.)
D. Derive the Stefan-Boltzmann law from the Planck
radiation law, as follows: The total
power per unit area radiated by a blackbody at a temperature T is ò0¥I(λ,T)dλ, where I(λ,T) is given by the Planck radiation law. Show that this is equal to σT4, where σ is a constant.
Hints:
-
Make the change of variable x = (hc)/(λkT).
-
Treat T as a constant in performing the integral.
- Use
the fact that ò0¥(x3dx)/(ex - 1) = π4/15
Your solution should show what σ is in terms of h, c, k and π.
ans:
σ = (2π5k4)/(15c2h3)
E.
1. (2 pts) If matter has a wave nature, why is this not observable in our daily
experiences?
2. (8) Let’s say that Planck’s radiation law was
![]() instead of the equation on the formula sheet. In this alternate universe, what would be the
relationship between lmax and T that would replace Wein’s displacement law? (lmax is the wavelength where I is a maximum. Treat T as a constant.)
instead of the equation on the formula sheet. In this alternate universe, what would be the
relationship between lmax and T that would replace Wein’s displacement law? (lmax is the wavelength where I is a maximum. Treat T as a constant.)
ans:
![]()
F. Estimate
the width of the n = 2 to n = 1 line in the spectrum of hydrogen as
follows. Background information: An
electron in the n = 2 state of hydrogen remains there an average of about 1.6 ns
before dropping to the n = 1 state. It
loses 10.2 eV as it falls. This 10.2 eV
becomes the energy of a photon given off by the atom.
a.
From the fact that it has this energy only 1.6 ns, what is the uncertainty in
the electron’s energy while in the n = 2 state?
(This would be the same as the uncertainty in the emitted photon’s
energy.)
b.
Write the relationship which gives a photon’s wavelength, λ, as a function of its
energy, E.
c.
Take the differential of this relationship between l and E to get a relationship between dl, the uncertainty in l, and dE, the uncertainty in E.
d.
Fill values into the expression from (c), including your ΔE from part (a). This is how far from the center of the line to either edge.
Multiply by 2 to get its width.
ans: 4.11 x 10 – 7 eV, 9.80 fm
Sec. 7 - Bohr Model of Hydrogen/X-Ray Spectra
Read:
A. The Kα line is the one emitted when an electron undergoes a transition from
the L shell (n = 2) to the K shell (n = 1).
Calculate the frequency of the Kα x-ray from a nickel target (Z = 28).
ans:
1.80 x 1018 Hz
B. 1. (2 pts)
Can the electron in the ground state of hydrogen absorb a photon of
energy (a) 10.0 eV? (b) 14.0 eV?
2. (8) What value of n is associated with the
94.96 nm line in the Lyman hydrogen series?
ans:
5
C. 1. (2 pts) Exciting an electron from the 1s
state to the 2s state requires about twice as much energy for a He+
ion as for a neutral helium atom.
Explain why.
2. (8) A tungsten target is struck by electrons
that have been accelerated from rest through a 40 kV potential difference. Find the shortest wavelength of the
bremsstrahlung radiation emitted.
ans: .0310 nm
D. 1. (2 pts) Suppose that the electron in a
hydrogen atom obeyed classical mechanics rather than quantum mechanics. Why would such an atom emit a continuous
spectrum rather than the observed line spectrum?
2. (8) In the Bohr model of hydrogen, what is
the wavelength of the electron in
a.
The ground state (n=1)?
b.
The first excited state (n=2)?
ans: 3.32 Ǻ, 6.65 Ǻ
E. A hydrogen atom is in its n = 2 state. According to the Bohr theory, this atom’s
radius is 2.117 Ǻ.
Using the Bohr theory, calculate
(a) the angular momentum of the electron,
(b) the linear momentum of the electron,
(c) the kinetic energy
(d) the total energy, E = KE + U
ans:
2.11 x 10-34kg×m2/s, 9.97 x 10-25kg×m/s, 3.40eV, -3.40eV
F. Atom
without a nucleus: PHY 132 will soon
cover how an electron in a magnetic field can follow a circular path. Such orbits have energy levels (called Landau
levels) similar to those in an atom. The
force on the electron is toward the center of its orbit and has a magnitude of F
= qvB where q is the charge, v is the speed,
and B is the magnetic field. Using this
in place of Coulomb’s law, repeat the procedure used for the Bohr atom in class
to find the radius of the allowed orbits from the electron’s deBroglie
wavelength. Show how the answer follows
from basic principles, not just the answer by itself. Express your answer in
terms of q, B, ![]() and n, where
n = 1, 2, 3 … (Like the Bohr model of
hydrogen, this approach to this system is not entirely accurate in all
details.)
and n, where
n = 1, 2, 3 … (Like the Bohr model of
hydrogen, this approach to this system is not entirely accurate in all
details.)
ans:
![]()
Sec. 8 - Wave Functions/The
Square Well
Read:
A. 1. (2
points) The two lowest energy levels in hydrogen are – 13.6 eV and – 3.4
ev. Use the uncertainty principle to
estimate how much time an electron can spend in a superposition of both states.
2. (8) A particle in an infinite square well of
width L is in the ground state, n = 1.
What is the probability of finding it the leftmost third of the well, 0 <
x < L/3? (Notice the table of
integrals in your formula handout.) ans: .1955
B. A
nucleus is often approximated by a square well.
Calculate the wavelength and energy of the photon emitted when a proton
goes from n = 2 to the ground state in a square well of width 10 fm (a typical
nuclear diameter.) ans: 202 fm, 6.14 MeV
C. 1. (2 pts) For a particle in a square well,
in an excited state, the probability density is zero at certain points between
the walls. Does this mean that the
particle cannot cross these points?
Explain.
2. (8) A particle with zero energy has a wave
function given by ![]() .
.
Find the potential energy function, U, as a
function of x.
ans:
U = (ħ2/m)(2x2 - 3)
D. The
wave function for a particle in a one dimensional box of width L is ψ(x) = A sin(nπx / L).
Use the normalization condition (which in this case becomes ò0L½y½2dx = 1) to find the
constant, A, in terms of L etc. (You must show a complete, step by step
solution for full credit.)
ans:
A = ![]()
E. 1. (2 pts) Use the uncertainty principle to
explain why a particle in a confined space has a zero-point energy.
2. (8) For
the n = 4 state of a particle in a one dimensional box of length L,
(a)
Sketch a graph of the probability density function from x = 0 to x = L.
(b)
Find the values of x where the probability density is a maximum.
(c)
Find the values of x where the probability density is a minimum.
ans:
max: x = L/8, 3L/8, 5L/8, 7L/8; min: x =
0, L/4, L/2, 3L/4, L
F. 1. (1
point) What is the maximum distance between two particles at which they can
remain entangled?
2. (9 points) A particle is free to move between
x = 0 and x = L, but at those points it encounters infinitely hard walls. Given that the solution to – ![]() = E
= E![]() is
is ![]() = A sin
= A sin 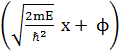 , where A and
, where A and ![]() are
constants, show how it follows from the boundary conditions that
are
constants, show how it follows from the boundary conditions that
- ![]() = 0 and
= 0 and
- the
energy levels are given by the expression on your formula sheet.
(That is, be able to repeat what I showed you in
class. Show a complete, step by step
solution.)
Sec. 9 - The 3-d Square
Well/Hydrogen
Read: Ch 42: sec. 4 – 6. Your text does not cover the 3 dimensional
square well, so be sure you have complete notes on this.
A. 1. (2 points) According to Bohr's theory, what is the
energy of a hydrogen atom in a 1s state?
According to the Schrodinger treatment, what is the energy of a hydrogen
atom in a 1s state?
2. (8) Find all possible values for L, LZ,
and θ for an electron in a 3d state of hydrogen.
ans:
L = ![]() ; LZ = -2
; LZ = -2![]() ,-
,-![]() , 0,
, 0,![]() or 2
or 2![]() ; θ
= 145°, 114°, 90°, 65.9° or 35.3°
; θ
= 145°, 114°, 90°, 65.9° or 35.3°
B. The radial
part of the wave function for an electron in a certain state of hydrogen is ![]() = A r
= A r ![]() where A is a constant and a0 is the
Bohr radius. Using this, calculate the
most probable value of r (the distance from the nucleus to the electron) in
this state.
where A is a constant and a0 is the
Bohr radius. Using this, calculate the
most probable value of r (the distance from the nucleus to the electron) in
this state.
ans:
4a0
C. In class, I found the two lowest energy levels
of an electron confined to a small cube.
For a cube 2.00 ![]() on a
side, (a) Find the next three energies
above those. (b) How many states are
there with each energy you found in (a)?
Give three answers – one for each energy.
on a
side, (a) Find the next three energies
above those. (b) How many states are
there with each energy you found in (a)?
Give three answers – one for each energy.
ans:
84.6 eV, 3 states; 103 eV, 3 states; 113 eV, 1 state
D. 1. (2 pts)
According to Bohr's theory, what is the orbital angular momentum of a
hydrogen atom in a 1s state? According
to the Schrodinger treatment, what is the orbital angular momentum of a
hydrogen atom in a 1s state?
2. (8) a.
Write out all possible combinations of the quantum numbers l and ml for a He+ ion (z = 2) with n =
3. Express each combination as a pair of
numbers: l, ml (b)
What is the energy of these states?
ans: l, ml = 0,0;
1,-1; 1,0; 1,1;
2,-2; 2,-1; 2,0;
2,1; or 2,2. Energy of all n = 3 states is -6.04 eV.
E. The ground state wave function for hydrogen
is ![]() =
= 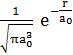 , where a0
is the Bohr radius. Show that this is
normalized.
, where a0
is the Bohr radius. Show that this is
normalized.
Hints:
-
You can’t have a negative radius.
Integrate from 0 to ∞, not – ∞ to
∞.
- At the upper limit of
integration (r = ∞), you will have a polynomial times an
exponential. An exponential dominates
over any polynomial at infinity. (Use the
value of the exponential and ignore the polynomial.)
F. For
convenience, work in a system of units where ![]() = 1. This makes hydrogen’s ground state wave
function
= 1. This makes hydrogen’s ground state wave
function ![]() =
= ![]() . What is
the probability of finding the electron between r = 0 and r =
. What is
the probability of finding the electron between r = 0 and r = ![]() ?
?
ans: .00793
Sec. 10 - Electromagnetic Waves
Read:
A. The
average intensity of solar radiation at the Earth (above the atmosphere) is
1340 W/m2. The average
Earth-Sun distance is 1.496 x 1011m.
Calculate
(a) the total power radiated by the sun.
(b) the maximum values of the radiation's
electric and magnetic fields at Earth.
ans:
3.77 x 1026W, 1.01 kV/m, 3.35 μT
B. 1. (1 point) .
Multiple choice: In classical physics, any time a charge accelerates, it gives
off ______.
a. electromagnetic radiation b. a constantly increasing magnetic field
c. electrons d.
a “displacement current”
2. (9) The electromagnetic wave is propagating
in the x direction. The wavelength is
50.0 m, and the electric field vibrates in the xy plane with an amplitude of
22.0 V/m.
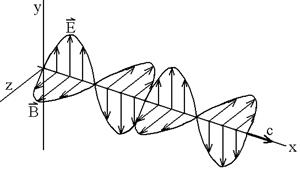 (a) Find its frequency.
(a) Find its frequency.
(b) Find the magnitude and direction of ![]() when the
electric field has its maximum value in the negative y direction.
when the
electric field has its maximum value in the negative y direction.
(c) Write a expression for B in the form B = Bmaxcos(kx-ωt).
ans:
6.00 MHz, –73.3 ![]() nT, B =
(73.3 nT)cos(.126x – 3.77 x 107t)
nT, B =
(73.3 nT)cos(.126x – 3.77 x 107t)
C. 1. (2 pts) Describe the physical significance
of the Poynting vector.
2. (8) A 4000 kg spaceship is to be propelled by
using a "sail" which reflects solar radiation. The sail is totally reflecting, oriented with
its plane perpendicular to the direction of the sun, and 1.00 km x 1.50 km in
size. What is the maximum acceleration
that the radiation can give this ship, if its intensity is 1340 W/m2?
ans: 3.35 mm/s2
D. 1. (2 pts) If you charge a comb by running it
through your hair, then hold the comb next to a bar magnet, do these electric
and magnetic fields constitute an electromagnetic wave?
2. (8) At a particular distance from the sun,
the rms value of the magnetic field caused by its radiation is 1.80 μT. For this solar radiation,
calculate
(a) the magnitude of the rms electric field.
(b) the average energy density.
(c) the average magnitude of the Poynting
vector.
ans:
540 V/m, 2.58 μJ/m3, 774 W/m2
E. A 15.0 mW helium-neon laser (λ = 632.8 nm) emits a beam of circular cross-section with a diameter of
2.00 mm.
(a) Find the maximum electric field in the beam.
(b) What total energy is contained in a 1.00 m
length of the beam?
ans:
1.90 kV/m, 50.0 pJ
F. From the equations describing an
electromagnetic wave, E = Emsin[(ω/c)x-ωt]
and B = Bmsin[(ω/c)x-ωt], and also from the relevant Maxwell equations
(in differential form),
¶E
= _ ¶B and ¶B = -μ0ε0 ¶E
¶x ¶t ¶x ¶t
show that the speed of light in a vacuum is c = 1 / ![]() . (Work
from just the relationships mentioned here.
The formulas on the formula sheet are what you’re supposed to be
proving.)
. (Work
from just the relationships mentioned here.
The formulas on the formula sheet are what you’re supposed to be
proving.)
Sec. 11 - Multi-Electron
Atoms/Molecules/Solids
Read: Skim Ch. 21 sec 3 ; Ch. 42 sec 7; Ch. 43 sec
2 – 6 (Just skim sec 3)
A. 1. (2 pts) An unexcited Boron atom contains two 1s electrons, two
2s electrons and one more. Give one of
the possibilities for the quantum numbers of this last electron. n = __, l = __, ml = __ & ms = __.
2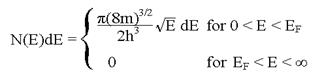 . At absolute
zero, the number of electrons in a metal per unit volume with energies between
E and E + dE reduces to
. At absolute
zero, the number of electrons in a metal per unit volume with energies between
E and E + dE reduces to
Use this and the
fact that n = ![]() to show that EF =
to show that EF = ![]()
B. 1. (2 pts) Why does a diatomic gas have a greater energy content per mole than a monatomic gas at the same temperature?
2. (8) Molecule Photon Frequency (Hz) Force Constant, k (N/m)
HI 6.69 x 1013 320
HF 8.72 x 1013 970
Use data from this table to calculate the minimum amplitude of
vibration for (a) the HI molecule, and (b) the HF molecule.
(c) Which has the weaker bond?
ans: .0118
nm, .00772 nm, HI is less stiff
C. 1. (2 pts) In a metal at room temperature,
a. About what percentage of
the states that are .5 eV below the Fermi Energy are occupied?
b. About what percentage of
the states that are .5 eV above the Fermi Energy are occupied?
2. (8) a. Write out the electronic configuration
for the ground state of sodium (Z = 11).
b. Write out the values for the set of quantum
numbers n, l, ml and ms for each electron in sodium.
ans:
a. 1s2 2s2 2p6 3s1 b. See solutions.
D. Sodium
is a monovalent metal having a density of .971 g/cm3 and molar mass
of 23.0 g/mole. Use this to calculate
a. the density of charge carriers, and
b. the Fermi energy.
ans:
2.54 x 1028 electrons/m3, 3.15 eV
E. A HCl
molecule is excited to its first rotational energy level, corresponding to J =
1. If the distance between its nuclei is
.1275 nm, what is the angular speed of the molecule about its center of
mass? Assume the isotopes involved are 1H
and 35Cl.
ans:
5.69 Trad/s
F.
Calculate the energy of a conduction electron in silver at 800 K if the probability of finding an electron in
that state is .950. The Fermi energy is
5.48 eV at this temperature.
ans:
5.28 eV
Sec. 12 - More on Solids/The
Nucleus
Read:
(The book does not include all I will cover
about superconductors, so be sure you have good notes.)
A. 1. (1½ pts) Put
“insulator,” “semiconductor” or “metal” in the blank.
- In a(n) __________, the highest energy
band containing electrons (the conduction band) is partly filled with many electrons.
- A(n) __________ has an empty
conduction band above a filled valence band.
- A(n) __________ has an empty
conduction band above a filled valence band at absolute zero, but the gap
between bands is narrow enough for some electrons to cross it at room
temperature.
2. (2 pts) Why do lattice imperfections and
lattice vibrations (phonons), which scatter electrons in normal metals, have no
effect on Cooper pairs?
3. (3½) A small permanent magnet is placed above a
superconductor. (a) What happens to the
superconductor to keep B = 0 inside of it?
(b) How does this explain the levitation of the magnet?
4.
(3) Find the radius of a nucleus of 23892U.
ans:
7.44 fm
B. 1.
(1.5 points) What happens to a superconductor when it is placed in a magnetic
field which is stronger than Bc, its critical magnetic field?
2. (1.5) A small cube of superconducting material would have energy
levels like those of a three dimensional square well. How many Cooper Pairs will be in the lowest of
these energy levels, E111?
3. (7) Using the fact that the atomic mass of 5626Fe is 55.934 940, find its
binding energy per nucleon.
ans: 8.79 MeV/nucleon
C. 1. (3 pts)
Explain what goes on in a p-n junction that allows current to flow
through it in one direction, but practically stops it from flowing the other
way.
2. (7) Light
emitted by hydrogen falls on a CdS crystal (energy gap = 2.42 eV). Which lines from the Balmer series are transmitted
through the CdS and which does it absorb?
(A substance’s band structure determines optical properties such as its color. CdS is orange because photons at that end of
the spectrum have too little energy to get an electron across the 2.42 eV gap
and are not absorbed. High frequencies do
have enough energy to excite electrons.
Remove blue from white light and orange is left.)
ans:
The n = 3 to n = 2 line is transmitted, all others absorbed.
D.
Consider a cube 1.30 mm on an edge, made of gold (Fermi Energy = 5.53
eV). Calculate the approximate number of
conduction electrons in this cube whose energies lie in the range 5.4900 to 5.4904
eV, at 300 K.
ans:
1.15 x 1016
E. 1. (2
points) The visible part of the spectrum
includes photons from about 1.8 eV to about 3.1 eV. At room temperature, silicon has an energy
gap of 1.14 eV and diamond has an energy gap of 5.47 eV. Explain why silicon is opaque but diamond is
transparent. (What happens when a photon
tries to interact with an electron in each material?)
2. (8) Consider a piece of gold (Fermi Energy =
5.53 eV). Calculate the approximate
number of conduction electrons per cubic meter whose energies lie in the range
2.00 to 4.00 eV, at 300 K.
ans:
2.35 x 1028
F. 1. (2 points) Silicon atoms each atom have
four electrons to use bonding with neighboring atoms.
a.
Explain why doping Si with phosphorous, which has 5 valence electrons, makes it
n-silicon.
b.
Explain why doping Si with boron, which has 3 valence electrons, makes it
p-silicon.
2. (2 pts) A common type of transistor is a pnp
or npn sandwich, whose center layer is very thin. Explain how this acts as a "valve"
for electric current.
3. (1) Is the center layer of a pnp transistor
doped with donors or acceptors?
4.
(2) How is it possible for all Cooper pairs in a superconductor to be in the
same quantum state?
5.
(1.5) What happens to the Cooper pairs in a superconductor if it is heated
above the critical temperature?
6.
(1.5) What sort of experiment first indicated that the atom has a small
positive nucleus, containing most of the mass?
Sec. 13 - Radioactivity &
Nuclear Reactions
Read:
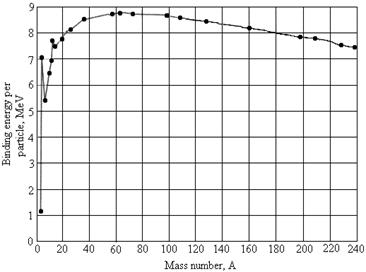
A.
1. (2 pts) Why are heavy nuclei unstable?
2. (8) Using this graph, estimate the energy
released when a nucleus of mass number 200 is split into two nuclei each of
mass number 100.
ans: about 180 MeV,
depending on how you estimate tenths of an MeV on the graph.
B. A
freshly prepared sample of a certain radioactive isotope has an activity of
10.0 mCi. After 4.00 h, its activity is
8.00 mCi.
a.
Find the decay constant and half life.
b.
How many atoms of the isotope were contained in the freshly prepared sample?
ans:
1.55 x 10-5s-1, 12.4 h, 2.39 x 1013
C. 1. (4 pts) Explain the difference between
alpha, beta and gamma rays. (I don’t
expect you to list every single way they differ, so various answers will be
considered correct.)
2. (6) Determine which decays can occur
spontaneously. Show why each answer is
correct.
(a) 4020Ca
® e+ + 4019K
(b) 9944Ru
® 42He + 9542Mo
(c) 14460Nd
® 42He + 14058Ce
ans:
Only (c) can occur.
D. Consider a sample of 23994Pu,
which has a half life of 24 120 years, and a mass of 1.00 kg at t = 0. Calculate
(a)
the number of 23994Pu nuclei present at t = 0,
(b)
the initial activity in the sample,
(c)
how much time until it reaches a "safe" activity of 0.100 Bq.
ans:
2.52 x 1024, 2.29 TBq, 1.07 Myr
E. 1. (2
pts) If a radioactive material has a half-life of one year, does this mean it
will be completely decayed after two years?
Explain.
2. (2) What is given off by the fission of
uranium that can go on to cause another fission event?
2. (6) Identify the missing nuclide or particle,
X. (If this is the quiz, a periodic
table of the elements will be printed on the back.)
(a) X
® 6528Ni + γ
(b) 21584Po
® X + α
(c) X
® 5526Fe + e+ + n
ans:
6528Ni, 21182Pb, 5527Co
F. 1. (4) In terms of biological damage, how
many rad of heavy ions is equivalent to 10 rad of x-rays?
ans:
.5 rad
2. (6) During a break, a technician decides to
heat 100 g of water for some coffee with his x-ray machine. If the machine produces 10.0 rad/s, what will
the water’s temperature increase be after five minutes? (The specific heat of
water is 4186 J/kg·°C.)
ans: .00717°C
Sec. 14 - Elementary
Particles/Cosmology
Read:
A.
1. (2 pts) What is an important difference between baryons and mesons?
2. (8) For each reaction, state the quark
composition of each particle, and the total number of up quarks, down quarks,
and strange quarks, both before and after.
(For example, count an up and an anti-up as a total of zero.) In part (d), identify the mystery particle.
(a) π-
+ p ® K0 + Λ0
(b) π+
+ p ® K+ + Σ+
(c) K-
+ p ® K+ + K0 + Ω-
(d) p
+ p ® K0 + p + π+ + ?
ans:
See solutions; Λ0
B.
1. (1 point) The muon was once known as the “mu meson.” Why did the name need to be changed?
2.
(2 pts) What is the source of the cosmic microwave background?
3.
(3) A distant quasar is moving rapidly away from the Earth. The shift in its spectral lines corresponds
to a speed of .160c. Determine the
distance from Earth to this quasar.
ans:
2.18 x 109 ly
4.
(4) Occasionally, high energy muons will collide with electrons and produce two
neutrinos according to the reaction μ+ + e ® 2n. What kind of
neutrinos are these?
ans:
![]()
C. Determine which of the following reactions
can occur. For those that can't, name a
conversation law which is violated.
(a) p
® π+ + π0 (e) π+ ® μ+ + ![]()
(b) p
+ p ® p + p + π0 (f) n ® p + e- + ![]()
(c) p
+ p ® p + p + π+
(d) p
+ p ® p + π+ (g) π+ ® μ+ + n
ans:
b, e & f can
D.
1. (1 pts) What is an important difference between hadrons and leptons?
2. (4) Name the four fundamental interactions, and the field particle
that mediates each.
3.
(5) Give the color and flavor of all the quarks in
a. A K° meson containing an antiblue ![]() quark.
quark.
b. A proton
containing a blue d quark and green u quark.
c. A muon.
ans. blue d & antiblue
![]() ; red u,
green u, blue d; none
; red u,
green u, blue d; none
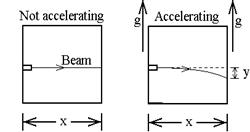
E.
1. In the absence of gravity, the beam of light follows a horizontal line when
the elevator is stationary. At t = 0,
the elevator acquires an upward acceleration of g. In terms of x, g and c, what is y, the
deflection of the spot on the wall?
(It’s simplest to consider a photon emitted at t = 0 and calculate the
distance the wall moves up while the photon is traveling.)
ans: y = - ½ g (x/c)2
2. In an
elevator at rest, what distance would a gravitational field of strength g bend
the beam downward?
ans: y = - ½ g (x/c)2
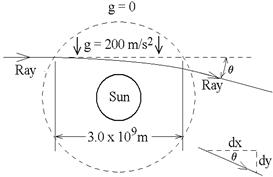
3. A crude model of the sun’s gravitational
field is shown. (No gravity outside the
dashed circle, a uniform field inside.)
Find the angle θ
by which the ray of starlight is deflected.
(Give a numerical value, not a formula.)
Hint: The ray’s path through the field is given by the function you
found in part 2. As shown at lower
right, tan θ
= dy/dx as the ray leaves the field.
ans: 6.67 x 10-6
rad, or 1.38” (similar to the
1.75”
observed in 1919.)
(There
is no quiz F this week.)