Experiment 6A: The Photoelectric Effect

BACKGROUND:

You will measure Planck's constant, and in the process verify the quantum theory of radiation.

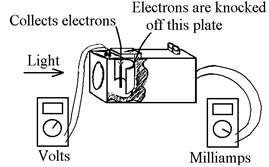
The apparatus contains a vacuum tube with a metal plate in it. Light falling on this plate knocks electrons off it, which travel through space and land on another piece of metal. The electrons then flow from the tube, through a circuit, and back into the tube to the plate where they started. The tiny current in the circuit is amplified then measured by a meter.

For several different wavelengths of light, you will determine the maximum kinetic energy the electrons get from the light, KE_max. This is done by seeing how much voltage is needed to turn them back before they reach the other electrode, stopping the photocurrent. (For example, if this "stopping potential" is 2 V, then KE_max is 2 eV.) According to Einstein, KE_max = hf - f. Since this is a linear equation, you should get a straight line if you plot KE_max as a function of frequency. From the slope and intercept of the line, you can get Planck's constant and the work function of the metal. The fact that the stopping potential depends on the light's wavelength, rather than its intensity, contradicts classical theory, but is a natural consequence of Einstein's concept that light is made up of photons.

To get the different wavelengths, you will use glowing helium, glowing mercury vapor and a He-Ne laser. The He and Hg sources emit only certain special wavelengths; the "lines" in its spectrum. To get a specific wavelength, you then remove other lines by passing the light through a filter. The wavelength for each source and filter are listed on the answer sheet. (In many cases, more than one spectral line actually gets through the filter. The shortest wavelength present is listed.) The laser is monochromatic, but a filter helps eliminate background light.

CAUTIONS: 1. Don’t touch the metal ends of the helium tube when it’s on; they’re at 5000 volts. Turn it off when not in use. Also, the tube can get hot.

2. The mercury lamp gives off ultraviolet radiation which is bad for your eyes. Lay a sheet of paper over the space between the lamp and the apparatus so you can’t look directly at the bulb.

3. The laser is intense enough to damage your eyes if it shines directly in.

EXPERIMENTAL PROCEDURE:

The basic idea is to slowly turn down the voltage from above the stopping potential, and watch for where a current first appears.

1. Plug in the photoelectric apparatus and turn it on before anything else, so the amplifier can start to stabilize. Also, turn on the computer and start it booting up.

2. Connect a digital multimeter, set to read DC volts to the nearest .01 V, to the voltage plugs on the apparatus. Connect another digital multimeter, set to read DC milliamps to the nearest .001 mA to the wires sticking out of the case. (The ammeter built into the case will read the same thing, but not as accurately.)

3. Select one of the light source/ filter combinations shown on the answer sheet. (Always have a filter on the photoelectric apparatus or you will be working with a mixture of frequencies instead of just one.) The long glass tube on a stand is the Helium source; the square gray thing with a round opening is the mercury lamp, and you know what the laser looks like. Use books or blocks of wood to get the light source and photoelectric apparatus to matching heights. Darken the room to eliminate other light sources.

- When using helium, aim the apparatus at the thin center part of the tube.

- Remember the sheet of paper with the mercury lamp.

- Lay the laser on its side on top of something about an inch and a half thick. The current seems to be largest when the beam enters the apparatus a little above center.

4. Turn the voltage knob (which controls the potential trying to turn back the electrons) all the way up, so you know you're above the stopping potential. Adjust the "zero adjust" knob so that the ammeter reads zero. It will probably wander by a few thousandths of a mA; you’ll have to live with that.

5. Turn the voltage down to zero and adjust the distance from light source to apparatus to obtain a current of 5.0 mA. (One setup won’t go that high. Use 1.5 mA with that one.) With the laser, distance isn’t much of a factor; it’s where the beam hits the tube. Play with it a little until you have around 5 mA. You may not be able to get 5 exactly. If it gives you too much trouble, passing the beam through a f = 5 cm lens placed two or three feet from the apparatus will spread the beam out, making the adjustment easier.

6. To observe what the stopping potential is: Turn the voltage knob up, stopping the photocurrent, then slowly turn it down, watching for the first sign of current flowing. The photocurrent starts out very small, so it can be hard to spot exactly where it starts because it’s masked by other effects. The ammeter can fluctuate a little at random, and also background light can make a small, gradually increasing current as you turn down the voltage. If the photocurrent is real, inserting a sheet of paper between the light source and the apparatus will make the current decrease. Double check. (Don't peek at the voltmeter, or you'll just go back to the same voltage you had the first time, right or wrong. Keep your eye on the ammeter until you decide you see that first little bit of current.) Don’t re-re-check now, it takes too much time. Try all the wavelengths, get the graph on the computer and look for points that don’t line up with the others. Then try again if any seem suspicious.

7. When you repeat with the other wavelengths, start each time by checking the zero and then readjusting the light to apparatus distance so that the current with V = 0 is 5.0 mA.

ANALYSIS:

1. From each wavelength, find the light's frequency.

2. From the potential needed to stop them, what is the maximum kinetic energy of the

photoelectrons in each trial? For convenience, you may leave this in electron-volts.

3. Have Excel plot maximum photoelectron energy, KE_max, as a function of the light's frequency, and calculate the best-fit slope & intercept:

a. Open Excel. Type the x values in column A and the y values in column B. The format for scientific notation is, for example, 3.6e17 for 3.6 x 10¹⁷. 3.6*10^17 will not work.

b. Draw a box around the numbers you want graphed. (If headings are in row 1, this would be columns A and B, rows 2 through 6.) Click Insert then Scatter then the option where nothing connects the dots.

c. On the Design tab under Chart Tools is a section called Chart Layouts. (If you don’t see Chart Tools, click on the graph to make it appear.) In Chart Layouts, click at bottom right to expand the choices and pick layout 9. (The layout number appears after a moment when you leave the curser on it.)

d. The axes should be labeled, including units. Click on the titles by the axes and type these in. Hit Enter.

e. The equation of the best fit line should have appeared on the graph, but the default settings don’t give enough significant digits. Right click on the equation, click Format Trendline Label, then under Category choose Scientific. Click Close.

4. If you have any points which are far off of the average line, go back to the apparatus and recheck them. Once everything is good, print a copy to include in your report.

5. From the slope and intercept of your graph, record Plank's constant and the work function of the metal. Due to the difficulty in deciding exactly when current begins to flow and also due to the small number of data points, the uncertainty in the slope is fairly large. Call it approximately + 25%.

6. In your conclusion, compare your value for h to the accepted one.

Also, comment on the fact that there's a clear relationship between stopping potential and frequency, a fact which cannot be explained by classical physics.

PHY 133 Experiment 6A: The Photoelectric Effect

	λ (nm)	f (Hz)	stopping pot. (V)	KEmax (eV)
Laser, red filter	633
Helium, yellow	588
Helium, blue	447
Mercury, blue	436
Mercury, green	546

h = ___________ + ___________

f = ___________