Experiment 10: Simple Harmonic Motion

Part 1: A mass on a spring.

You will verify that the period of a harmonic oscillator is given by T = 2π and that its displacement is given by x = A cos ( t + f). The spring constant, k, is found by observing how much the spring is stretched by a weight, and applying Hooke's law. A known mass is then hung from the spring above a motion sensor connected to a computer. By timing reflected sound waves, the computer produces a graph of position versus time, from which the period is read and compared to the formula’s value. The graph itself is compared to the curve from the formula for x.

Procedure:

Don't bother with uncertainties in each step. To save time, you will be given a figure at the end.

1. Determine the spring constant:

Hang the spring vertically. Put enough weight on it to begin stretching it (a few grams, without a hanger). The spring is tightly wound, so the coils press against each other and a certain minimum force is needed to start stretching it.

Then, measure how much additional displacement, Δx, is caused by some additional weight, ΔF. The larger the displacement the smaller the percentage of uncertainty, so something like 50 g that stretches it a lot is good. Show how k is found from this data in the space provided.

2. Connect the interface to a computer and a motion sensor. Use the motion sensor to record at least one complete period, with a 50 gram hanger on the spring. (The hanger's large bottom reflects more sound than a slotted weight.)

Open PASCO Capstone on the computer. Click Hardware Setup at the upper left. Click the yellow circle by Input 1 then Motion Sensor II. Click Hardware Setup again.

In the column on the far right, double click Graph, which is at the top. Click <Select measurement> by the vertical axis and select Position (m).

Hang the oscillator as far over the edge of the counter as possible, at least 15 cm, to avoid sound reflecting off the counter. The bottom of the hanger needs to be fairly horizontal, so it doesn't reflect the sound off to the side. Put the sensor on the floor, aimed at the oscillator from below. The motion should bottom out no closer than 40 cm away.

To adjust the graph so that x = 0 is the equilibrium position, get the mass to hang as still as possible. Click REC at the lower left of the screen. Click at the bottom, just to the right of center. Click STOP.

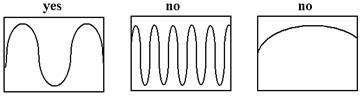Get the oscillator moving, then record data for at least one period. Change the graph’s scale to show from somewhat before the first peak to a little after the next one. If it does not look like a good cosine wave, look for the problem and make another run. Once you have a good graph, pick up the sensor before someone steps on it.

Save the file, then print copies of the graph for everyone in your group by connecting the laptop to the printer on the cart. It comes out better in landscape mode rather than portrait. If you need to wait for the printer, you can go on to the next step in the meantime.

3. Read the period of oscillation from the graph. To measure differences between two points on graph, click on at the top of the graph. Move the crosshairs to the point at the start of your interval. Right click then select Show Delta. A rectangle appears. Move its opposite corner to the point at the end of the interval. Δx, written above the rectangle, is the difference in time. Δy, written beside it, is the difference in position.

4. Now, calculate the period from the formula. You have the spring constant from step 1. For the mass, use the suspended mass plus one-third of the spring's mass.

5. Determine the phase angle, f: From the graph, read the time of the first peak to the right of the origin, t₁. (This is easiest using the crosshairs from step 3.) f = – (2π / T) t₁. They should be about the same anyhow, but let's say to use the experimental T in that.

6. Plot the theoretical equation, x = A cos ( t + f), by hand on the same graph: Use the table provided to calculate the displacement every .2 second for one period, then plot and connect the points. k and m are the same as you used in calculating T. Label this curve "theoretical".

Assume the uncertainties in both the measured and calculated periods are 2% each. Does the theoretical period agree with the observed one? (As usual, if they don't, explain why not.)

Comment on how well the theoretical equation represents the experimental curve.

Part 2: Large amplitude pendulum.

The period of a large amplitude pendulum will be measured with a stopwatch and compared to the relationship T = 2π.

Remove the spring from the support stand, and replace it with a mass suspended from a string at least 50 cm long. The horizontal support should now be at the top of the pole. Pull the pendulum to the side so that the string is nearly horizontal, and release it. If it goes to the side and hits the counter before you’re done, be more careful to release it without pushing to the side or spinning it. The way you hold the ball before releasing it should be the same on both sides of it: For example, try releasing it from between both hands. Or, hold the ball cradled in your fingers, and then open them to let it fall between the middle ones.

Time its period with a stopwatch, to an accuracy of + 3% or better: You make errors both starting and stopping the watch. For most people, these errors would add up to half a second or less. So, you need to time a large enough number of periods so that .5 s is less than 3% of the time the stopwatch runs. (But, don't go more than about 15 periods, or the air drag will reduce the amplitude too much.) Then, divide to get the time for one period.

Measure the length of the pendulum to the center of its mass, and calculate the period from the formula, using 9.80 m/s² for the local value of g. Assuming g has a negligibly small uncertainty, the percent of uncertainty in this T is half of that in l, due to the square root. Do the measured and calculated periods agree? (As usual, if they don't, explain why not.)

PHY 131 Experiment 10: Simple Harmonic Motion

Part 1:

1. ΔF = _______________ Δx = _______________

Calculate k:

2. (Attach your graph)

3. Measured T = _______________

4. m_hanging = 50 g, m_spring = _______________ (1/3 m_spring = ______________ )

Calculated T = = _________________ .

5. t₁ = _______________. Calculate f:

Fill in the numbers:

t (s)

theoretical x (m)

Part 2:

No. of cycles = _________, t = _________ ± .5 s, measured T = _________ ± _________

length = __________ ± __________ calculated T = __________ ± __________