Experiment 2: Vectors

In this lab, you will verify that the net force on an object in equilibrium is zero. Three scales, calibrated in newtons, are hooked to a metal ring. They are put under tension to create forces on the ring. Reading the scales gives the magnitudes of the forces; tracing the scales on a sheet of paper records the directions. You then determine the resultant, using two different methods, to see if it agrees with zero.

PROCEDURE: Hook the scales to the ring, and put the chains on their other ends in the notches on the metal circle. The forces should all be at least 5 N, and should all be different from each other.

Slide a blank sheet of paper under the scales and trace them to record their directions. Record the magnitude of each force on the paper, estimating to the nearest tenth of a newton. Each person in your group should take their own data. However, there is no need to rearrange the apparatus for each person.

Draw a line up the middle of each scale's outline, and put an arrowhead on the end. Label the forces , and . Draw an x-axis along and a y-axis perpendicular to it. Measure the angle of each force, showing the results directly on the sheet.

ANALYSIS. (As with all labs, everyone in the group should do the following themselves. However, this isn't a test; you should ask each other questions and correct each other's mistakes.)

Find the resultant two different ways:

1. Graphically. On another sheet of paper, find the resultant of your three forces by drawing them to scale, head to tail, then drawing their resultant. Lined paper, such as notebook paper, is the most convenient, although unlined paper will work. (Theoretically, the three forces should form a closed triangle, but in practice, there is usually a small nonzero resultant because of experimental errors.)

A larger diagram is more accurate, so choose a scale which fills most of the page. The scale should be written on the diagram. (For example, 1 cm = 20 N.) Don't bother finding an uncertainty with this method. To save time, just assume it is + 1.5 N.

2. Component method. Calculate the components, and put them in the table provided. Use them to find the components of the resultant. Include the uncertainty with each step. Some comments to help with the uncertainties:

a. These particular scales give the magnitude of each force to about +.5 N, due to how closely you can read the scale, and also their calibration. For the directions, assume + 1 degree, due to how accurately you drew the lines, and how closely you can read the protractor.

b. The direction of was not measured; we defined the x axis to lie along it. So, the uncertainty of its x component is just the uncertainty of the scale, + .5 N. The y component is not based on measurement at all, so its uncertainty is + 0.

c. The components of and are calculated from two measurements, the scale and the protractor. The rule about adding percents is for when only multiplication or division are involved, and does not apply here because of the trig function. The general rule that applies to any calculation is to approximate the small difference between the true value and what you might have gotten by a differential. (The other rules you were given can be derived from this.)

(If you don’t understand differentials or don’t care where the formulas came from, skip this box.)

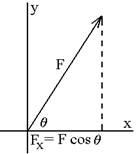
F_x = F cosq

Using the product rule to take the differential,

dF_x = F(-sinq dq) + (dF)cosq

where the dq in the first term is from the chain rule.

Any differential is positive if it represents an increase, negative for a decrease. F_x would be farthest off if dq was negative and dF was positive, which would cancel the minus by the sine and make the two terms add rather than subtract. So, the uncertainty is dF_x with the minus sign thrown away.

Uncertainty in F cosθ =

Similarly, it follows from differentiating F_y = F sinq that

Uncertainty in F sinθ =

These formulas assume q is in radians. For people reading angles from protractors, degrees is more convenient. Converting to degrees gives the versions below.

Uncertainty in F cosθ =

Uncertainty in F sinθ =

where dF = uncertainty in F and dθ = uncertainty in θ in degrees.

(“d” actually means a vanishingly small difference. It is being used not quite correctly here for a difference which is small but finite.)

Example: To find the x component of the force shown:

The size of the uncertainty shows that the last significant digit is the tenths place, but it’s a good idea to carry an extra digit until you get to the final answer.

d. Once you have the components of all three forces and their uncertainties, find the components of the resultant. Find their uncertainties with the rule from lab 1A.

Conclusion: In your conclusion, say whether + + = is true, within experimental uncertainty. That is,

- Does each component of the resultant agree with 0?

- Does the resultant from your scale drawing agree with 0?

PHY 131 Experiment 2: Vectors

(attach sheet you slid under balances)

_____________________________________________________________________________

Graphical (head - to - tail) method:

(Attach solution, or do it on the back)

Answer: __________ N at __________ degrees.

_____________________________________________________________________________

Component method:

	x-components	y-components
	± .5 N	0 ± 0 N
	±	±
	±	±
+ +	±	±

Sample calculation: In the space below, show step-by-step how you calculated both components and both uncertainties you show for .