Experiment 6: Conservation of Energy and Momentum in a Collision

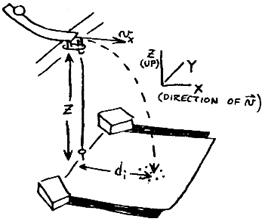You will check for conservation of kinetic energy and for conservation of momentum in a collision between two ball bearings. One ball bearing is rolled down a ramp. You let it fly off to find its speed at the end of the ramp, indicated by how far away it lands. Where it lands is recorded by it hitting a sheet of paper laid over carbon paper. The ball bearing is then rolled down again, this time with an identical ball sitting at the end of the track. After colliding, they fall to the floor, again landing on paper over carbon paper. The velocity of the one ball as it reaches the end of the ramp is used to find the energy and momentum just before the collision; the velocities of the two balls just after they hit are used to find final energy and momentum.

PROCEDURE: Measure the mass of both ball bearings. They should be identical. Lay the carbon paper on the floor, carbon side up, and put a sheet of 18” by 24” paper on top, with the plumb bob hanging over the middle of the shorter side. (“Plumb” means vertical the same way that “level” means horizontal. The “bob” is the weight on the end of the line.) Weight the paper down.

Mark the point under the plumb bob.

Adjust the screw at the end of the track which the target ball will sit on:

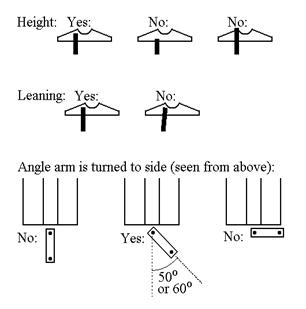a. Get your eye exactly level with the countertop. Then, adjust the screw so that its top is at the same height as the bottom of the groove in the ramp. This way, the incident ball will knock the target ball cleanly off the screw.

b. Check that the screw is not leaning to one side; it should look like a fatter extension of the plumb line.

c. The arm should be turned about 50° or 60° to the side, otherwise one ball won’t be going fast enough to miss hitting the arm as it falls. In a trial collision, check that both balls land at least 10 cm from the plumb bob (hopefully more). If necessary, readjust the angle that the arm makes. Then, recheck the screw’s height.

Once adjusted, be careful not to bump it; the arm can be kind of floppy. Remember where you released the ball; it must be the same throughout the experiment.

Without the target ball in place, release the other ball at least half a dozen times. Don’t move the paper the balls land on yet.

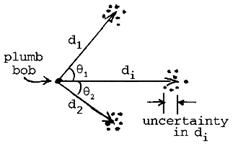
The screw has a dimple for the target ball to sit in. Put the target there and try a collision. d₁ and d₂ should be fairly similar to each other. 10 cm is the absolute minimum for each of them so that the falling balls clear the arm. Do at least another half dozen trials. Have the instructor check the results before going on.

Turn the paper over to see the dots better. Measure the distance from the plumb bob to each cluster of impact points. The amount 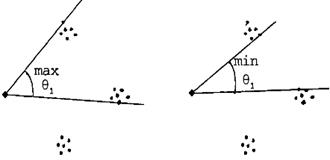of scatter in the dots shows you the uncertainty: For example, if the closest dot is at 24.2 cm and the farthest is at 27.6, record the distance as 25.9 + 1.7 cm. Also, measure the angles θ₁ and θ₂. For example, if "max θ", as shown, was 60°, and "min θ", was 50°, then you would record the angle as 55 + 5°. Also, measure the vertical height of the fall, z.

Calculations: Show how to set each calculation up in the space provided. Do not over-round: A zero used only to show where the decimal point goes is not significant. To have three significant digits, you need something like .00437 not .004.

Compute the time to fall to the floor: The vertical component of the ball’s motion obeys

z = v_zit + ½a_zt²

In this case, v_zi = 0 because the ball is moving horizontally at the end of the track. Also a_z = g, taking down as positive. With these substitutions,

z = 0 + ½gt² Solving, we obtain

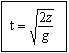
The uncertainty in t is very small; accurately enough we can call it zero.

Next, find v_i, the speed the first ball has at the end of the ramp. Once it becomes a projectile, the horizontal component of its velocity doesn’t change, so its speed at the end of the ramp equals its average horizontal speed while flying: v_i = d_i/t. From this, compute the kinetic energy of the first ball before the collision. Find the uncertainties with the usual rules. Either leave uncertainties as percents or convert as indicated by the blank; the choice was based on what you will need next.

Find v₁ and v₂ the same way you found v_i. From them, find the system’s total kinetic energy after the collision.

Now, check for conservation of momentum. Momentum is a vector, so think in terms of components:

- Find the magnitude of the momentum before the collision, p_i. Assuming no uncertainty in mass, p_i will have the same percent uncertainty as v_i. Then, write what its x and y components are. ( points directly along the x axis.) Include each component’s uncertainty, in units of momentum, calculated from the percentage.

- Find the magnitude of each ball’s momentum after the collision, p₁, and p₂.

- Find the components of and , showing how in the space provided. Pay attention to + and - signs.

- Finding the uncertainty in a vector’s components from the uncertainties in its magnitude and direction was discussed in lab 2. By a similar procedure (approximating the uncertainty as a differential without minus signs),

Uncertainty in p cosθ =

Uncertainty in p sinθ =

where dp = uncertainty in p and dθ = uncertainty in θ in degrees.

(“d” actually means a vanishingly small difference. It is being used not quite correctly here for a difference which is small but finite.)

- Write the total final momentum, , as a vector.

Conclusions: Within the uncertainty, was kinetic energy conserved? (Don’t be surprised if a little energy was lost. Realistically, the collision is slightly inelastic.) Was the x component of the momentum conserved? Was the y component of the momentum conserved?

Please put the ball bearings back in their box. They tend to get lost otherwise.

PHY 131 Experiment 6: Energy and Momentum in a Collision

DATA:

m = __________ + 0 (uncertainty small enough to ignore.)

d_i = ___________ + ___________ (percent uncertainty = ____________%)

d₁ = ___________ + ___________ (percent uncertainty = ____________%)

d₂ = ___________ + ___________ (percent uncertainty = ____________%)

θ₁ = ___________ + ___________

θ₂ = ___________ + ___________

z = ___________ + 0 (also small enough to ignore.)

COMPUTATIONS:

Compute t:

Just before collision:

v_i = = ___________ + ___________ %

KE_i = = ___________ + ___________J

Just after collision:

v₁ = = ___________ + ___________%

v₂ = = ___________ + ___________ %

KE₁ = = ___________ + ___________ J

KE₂ = = ___________ + ___________ J

KE_f = ___________ + ___________ J

Magnitude of p_i = = ___________ + ___________ kg×m/s

= ( + ) + ( + ) kg×m/s

Magnitude of p₁ = = ___________ + ___________ kg×m/s

Magnitude of p₂ = = ___________ + ___________ kg×m/s

p_1x = ___________ + ___________ kg×m/s

p_2x = ___________ + ___________ kg×m/s

p_1y = ___________ + ___________ kg×m/s

p_2y = ___________ + ___________ kg×m/s

= ( + ) + ( + ) kg×m/s