Experiment 8: Equilibrium

Part 1:

You will see if the total torque on a stationary object is zero. Three scales, calibrated in newtons, are hooked to a wooden block. They are put under tension to create forces on the block. Reading the scales gives the magnitudes of the forces; tracing the scales on a sheet of paper records their lines of action. Moment arms from an arbitrary point are measured on the tracing, and the torque from each force calculated. The total is then compared to zero.

Procedure: With spring scales, apply three different forces of at least 5 N to the wooden block. Slide a sheet of paper under the block. Trace the block and the scales. Record the magnitude of each force on the paper, estimating to the nearest tenth of a newton. Each person in your group should take their own data. However, there is no need to rearrange the apparatus for each person.

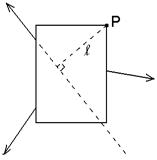
Take the paper off the apparatus. Draw the line of action of each force down the center of the scales, and all the way across the paper, including arrowheads to indicate the direction. (The three lines of action must meet at one point.) Label one corner of the block as point P. Draw each force’s moment arm, the perpendicular distance from P to its the line of action. (You can use the corner of the ruler to draw a 90° angle.) Measure each moment arm in centimeters and record it on the diagram. The uncertainty in your data is .5 N for the spring scales, and your own estimate for the ruler.

Under Calculations, find the torque of each of the three forces about the axis at P, and their uncertainties. Include step-by-step calculations in the space provided. To decide whether a torque is positive and which negative, it might help to press down on point P with your pencil point so that you can actually rotate the sheet about that point. Then, notice which way the sheet turns when you push along the line of action in the direction of the force. Find the total torque and its uncertainty. Is the total torque about P equal to zero, within experimental uncertainty?

Part 2:

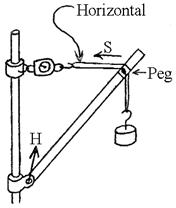
You will calculate the string tension, S, in the model crane shown, and see if it matches the reading on the scale along the string. You will also calculate the force, H, from the hinge at the lower end, but won’t check it experimentally. The crane is made from a half-meter stick mounted on a ring stand as shown. The weights and dimensions of the apparatus are measured, then the string tension, S, is calculated using the second condition of equilibrium.

Data.

To save time, instead of calculating uncertainties, just wait until the end, and then assume that computed value of S is good to + 5%, and the uncertainty in the measured value is .5 N.

Remove the boom from the crane and hang it from the spring scale to measure its weight, including the metal clips. Calculate the weight of the load you will hang from it from the mass, which should be at least 300 grams.

Locate the boom's center of gravity (including the clips) by seeing where it balances on your finger. Remember where it is so you can find it later.

Reassemble the crane: Set its lower end in place. Then, hook the loop of string to the newton scale, pass it over the pegs near the top of the boom, and hang the load from the other end. You might want to wind the string around the pegs so it can't slip. Be sure the string is horizontal, as shown.

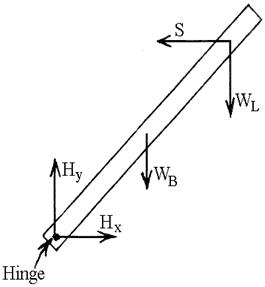
Measure the moment arms. This is just like part one: For each force, measure the distance from the hinge to the force's line of action along a perpendicular. (Calculating from the length along the boom and an angle is the hard way.) For W_B and W_L, you might want to use a string with a weight on the end to help you judge where the line of action is. Show each moment arm on the picture on the data sheet, including arrows to show from where to where you measured.

Calculations:

Use Στ = 0 to solve for the string tension, S. Note that S is the unknown you're solving for; do not fill in the measured value. Show all steps of the calculation in the space provided.

Use ΣF_x = 0 to find H_x, the x component of the force from the hinge. Similarly, use ΣF_y = 0 to find H_y.

Now, read the spring scale to obtain the measured value of S. Does the computed value agree with this measured value?

PHY 131 Experiment 8: Equilibrium

PART ONE:

(Attach sheet that you slid under block.)

Calculations:

τ₁ =

τ₂ =

τ₃ =

Total torque =

PART TWO:

Boom Weight = ________________

Load Mass = __________________

Load Weight = ________________

On the diagram, use arrows to show

from where to where you measured

each moment arm.

Calculations:

Στ = 0

ΣF_x = 0

ΣF_y = 0

Measured value of S = ______________________